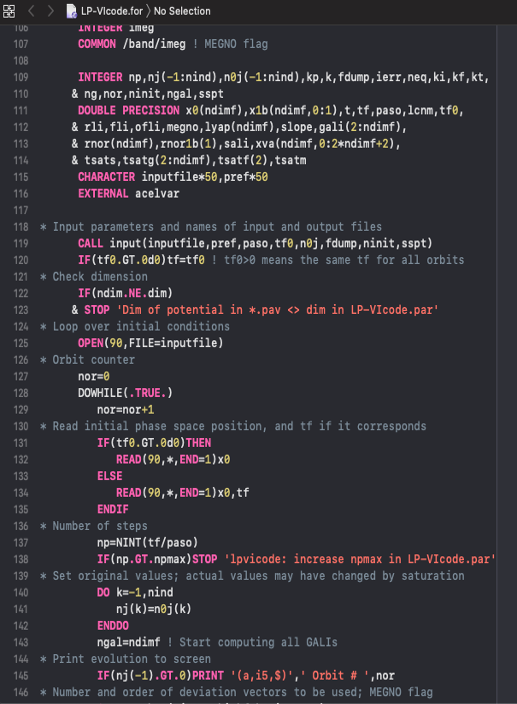
The suite's kernel code. A program to compute the 10 most worldwide used chaos indicators based on the evolution of the deviation vectors as well as many physical and geometrical orbital properties. Also, the LP-VIcode current version: "Control" is NEMO friendly. A front-end is under developing stage. Click here for further details.
Loading...
The LP-VIsuite Project
The La Plata Variational Indicators Suite (LP-VIsuite) is an OPEN-SOURCE software specifically designed to compute a plethora of variational chaos indicators on user-defined potentials.
The suite also includes a ready-to-use realistic Milky Way-type galaxy potential.
The suite also includes a ready-to-use realistic Milky Way-type galaxy potential.
Current state
The current version of the suite is composed of the LP-VIcode (version 2.0.2, codename "Control"), Smart (v. 1.2.3) and MilkyWayHydra (v. 2.0).Library
The LP-VIcode includes the 10 most worlwide used variational chaos indicators.Automatic differentiation
Smart can compute automatically accelerations and variational equations on generic potentials.A synthetic galaxy
MilkyWayHydra is a realistic Milky Way-type galaxy potential with accelerations and variational equations already computed and validated to be used right out of the box.Parallelization
A parallel version in Fortran90 of the kernel code LP-VIcode is on a developing stage.MilkyWayHydra 3.0
A fully time-dependent MilkyWayHydra update with also new components to select is still ongoing work.User-friendly: help us!
We welcome developers that want to help us with making the suite more user-friendly, for instance changing the programs' command-driven interface to a menu-driven interface.Library+: help us again!
Researchers that want to add their own variational chaos indicators to the present library of the suite are also welcome to do it.The LP-VIsuite Components
Kernel "LP-VIcode" + slave "Smart" + potential "MilkyWayHydra"
The LP-VIsuite
The LP-VIsuite is a software package composed of three basic elements. The kernel code, "LP-VIcode";
the automatic differentiation pre-processing slave program, "Smart" and a ready-to-use realistic Milky Way-type galaxy potential, "MilkyWayHydra".
the automatic differentiation pre-processing slave program, "Smart" and a ready-to-use realistic Milky Way-type galaxy potential, "MilkyWayHydra".
LP-VIcode
SMART
The slave program. The Smart module is an automatic differentiation program that was first conceived to be used as a pre-processing stage of the LP-VIcode. It computes the accelerations and variational equations with the only input of the potential function. That is, there is no need to calculate manually the accelerations and variational equations any more.
MilkyWayHydra
The ready-to-use potential. The current version of the MilkyWayHydra is a fully modifiable seven-component and exhaustively detailed Milky Way-type galaxy potential. It comes with the accelerations and variational equations already computed and validated to be used right out of the box with the LP-VIcode.
The LP-VIsuite main features
See below our goal and a short introduction of the main features
Goal
The correct analysis of a given dynamical system rests on the reliable identification of the chaotic or regular behaviour of its orbits. The most commonly used tools for such analyses are based either on the study of the fundamental frequencies of the trajectories, or on the study of the evolution of the deviation vectors, the so-called variational chaos indicators. Therefore, it seems very useful to have a software with which one can compute several variational chaos indicators in an easy and fast way. This is the main gaol of the LP-VIsuite package.
A wordlwide used library of chaos indicators
The library of variational chaos indicators in the present version of the suite includes the following:
LI
The Lyapunov Indicators, a.k.a. Lyapunov Characteristic Exponents, Lyapunov Characteristic Numbers or Finite Time Lyapunov Characteristic Numbers (LIs; Benettin et al. 1976, Benettin et al. 1980).
MEGNO and SElLCE
The Mean Exponential Growth factor of Nearby Orbits (MEGNO; Cincotta and Simó2000, Cincotta et al. 2003). The Slope Estimation of the largest Lyapunov Characteristic Exponent (SElLCE; Cincotta et al. 2003).
SALI and GALI
The Smaller ALignment Index (SALI; Skokos 2001). The Generalized ALignment Index (GALI; Skokos et al. 2007, Skokos et al. 2008).
FLI and OFLI
The Fast Lyapunov Indicator (FLI; Froeschlé et al. 1997, Lega and Froeschlé 2001). The Orthogonal Fast Lyapunov Indicator (OFLI; Fouchard et al. 2002).
SD
The Spectral Distance (SD; Voglis et al. 1999).
SSN
The dynamical Spectra of Stretching Numbers (SSNs; Voglis and Contopoulos 1994, Contopoulos and Voglis 1996).
RLI
The Relative Lyapunov Indicator (RLI; Sándor et al. 2000, Sándor et al. 2004).
The main achievement of the suite's kernel code, the LP-VIcode, is its speed. Neither the orbit nor any of the sets of variational equations are computed more than once in each time step, even when they may be requested by more than one variational chaos indicator.
A Complete Automation Resource
The main achievement of the suite's companion codes, the Smart automatic differentiation pre-processing slave program and MilkyWayHydra, a ready-to-use Milky Way-type galaxy potential, are the complete automatization of the input routines necessary for the kernel code to compute the variational chaos indicators.
Smart can compute automatically the accelerations and variational equations given a generic user-defined potential function offering you the chance to study any potential you like.
In case you are a researcher in the field of galactic dynamics, MilkyWayHydra offers you a fully modifiable multi-component and realistic Milky Way-type galaxy potential with the input routines already computed and validated to use it with the kernel code right out of the box.
Smart can compute automatically the accelerations and variational equations given a generic user-defined potential function offering you the chance to study any potential you like.
In case you are a researcher in the field of galactic dynamics, MilkyWayHydra offers you a fully modifiable multi-component and realistic Milky Way-type galaxy potential with the input routines already computed and validated to use it with the kernel code right out of the box.
Papers
The literature behind the development of the LP-VIsuite
LP-VIcode: origins
The PhD thesis that presents a thoroughly comparative study of the most used chaos indicators in the literature, which includes a series of papers where the earliest versions of the LP-VIcode were applied.
LP-VIcode: the alpha version
The paper that introduces the first version of the LP-VIcode.
LP-VIcode: the first stable version
The paper that fully describes the completely rewritten and first stable version of the LP-VIcode, version 1.0.2. codename "Kaos".
Smart & MilkyWayHydra
The paper that fully describes the first stable version of the automatic differentiation program Smart, version 1.2.3 and that introduces the validated ready-to-use seven-component Milky Way-type galaxy potential, MilkyWayHydra version 2.0.
Downloads
Here you can freely download the current version of the suite's programs as well as all the related documentation
LP-VIcode: User Guide
- Latest version, 2.0.2
- Step by step configuration, compilation and execution
- Full and easy examples to follow
LP-VIcode: Examples
- The 2D Henon-Heiles potential
- The 2D Logarithmic potential
- A 3D triaxial extension of the Navarro-Frenk-White dark matter halo potential
MilkyWayHydra:
Descriptive Memory
- Latest version, 2.0
- An exhaustively detailed document on the MilkyWayHydra code
Before you download and go, please take a look at the ongoing and future developments below!
ONGOING IMPLEMENTATIONS AND FUTURE DEVELOPMENTS
ONGOING IMPLEMENTATIONS: Version 3.0 of the MilkyWayHydra is ongoing, time growth for every component of the model is being coded as well as new component options to build a more personalized galaxy. A parallel version of the LP-VIcode entirely written in Fortran90 is on a developing stage.
FUTURE DEVELOPMENTS: A menu-driven interface to make the LP-VIsuite more user-friendly is on an early developing stage.
MilkyWayHydra 3.0
PARALLELIZATION
MENU-DRIVEN INTERFACE
HOW TO CONTRIBUTE: GET IN TOUCH
The main goal of the LP-VIsuite project is to cluster in a single, easy-to-use software the plethora of variational chaos indicators that are nowadays in the literature. We intend to motivate researchers to collaborate with their own methods in developing newer versions of the suite with larger variational chaos indicators' libraries. You can also make suggestions to improve the suite or report a bug.
Or just in case you want to get in touch with us, please fill the form below and we will contact you as soon as possible. Thank you!
And Last but not Least: Meet Our Team
The Chief
Dynamics of stellar and planetary systems
Daniel Carpintero
FCAGLP-IALP
Hymie
Formation and evolution of planetary systems
Luciano Darriba
FCAGLP-IALP
86
The impact of chaos in Milky Way-type galaxies
Nicolás Maffione
UNRN-CONICET
